Measurement Uncertainty (MU) relates to the margin of doubt that exists for the result of any measurement, as well as how significant the doubt is. For example, a piece of string may measure 20 cm plus or minus 1 cm, at the 95% confidence level. As a result, this could be written: 20 cm ±1 cm, with a confidence of 95%. Therefore, we are 95% sure that the piece of string is between 19 cm and 21 cm long.

Standards such as ISO 15189 require that the laboratory must determine uncertainty for each test. However, they have not specified how this should be done.

How do we calculate Measurement Uncertainty using QC data?

Employing your QC data to calculate uncertainty makes several assumptions; your test system is under control, the patient samples are treated in the same manner as your controls and gross outliers have been removed. If you choose to use your QC data to calculate this you should ensure that you use a commutable control with a matrix similar to that of a patient sample, with analytes present at clinically relevant levels

To calculate MU, labs must look at the intra-assay precision and inter-assay precision of their test.

Intra-assay precision: Sometimes known as ‘within run’ precision, is where 20 or more replicates of the same sample are run at the same time, under the same conditions (calculated from a single experiment). Intra-assay precision helps to assess systematic uncertainties

Inter-assay precision: Sometimes known as ‘between run’ precision, is where 20 or more replicates are run at different times – e.g. 1 replicate every day for 20 days (can be calculated from routine IQC data). Inter-assay precision can help identify random uncertainties within the test system.

*The Australian Association of Clinical Biochemists (AACB) recommends that at least 6 months’ worth of QC data are used when calculating the inter-assay precision¹.

Once the data is collected, you must calculate the standard error of the mean (SEM) of the intra-assay precision (A) and the SD of the inter-assay precision (B) in order to measure the uncertainty (u). Once A and B have been calculated, they need to be squared, added together and the square root of the sum found:

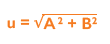
As uncertainty is calculated as SD and 1SD is equal to 68% confidence on a standard Gaussian curve, we can conclude that if we multiply using a coverage factor of 2, we can attain 2SD confidence of 95%. This is known as the Expanded Uncertainty (U):

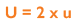
What is the Advantage of Measurement Uncertainty for a lab?

Labs need to carry out MU as it is a requirement of ISO 15189. It states: “The laboratory shall determine measurement uncertainty for each measurement procedure, in the examination phases used to report measured quantity values on patients’ samples. The laboratory shall define the performance requirements for the measurement uncertainty of each measurement procedure and regularly review estimates of measurement uncertainty”.

MU also helps determine whether the difference between two results is negligible due to uncertainty or significant due to a genuine change in condition of the patient; giving labs a greater confidence in reported results.

How can Randox help?

Our new Acusera 24.7 Live Online software provides automatic calculation of MU, saving valuable time and helping labs meet ISO 15189 requirements with ease.

Contact marketing@randox.com to find out how your lab can benefit from Acusera 24.7 Live Online